Unable to debug dll source code with symbol server

Posted on 2 mins read

I’ve blogged in the past about using a Symbol server and I recommend to all people to use symbol servers whenever possible , to helping people troubleshooting problem on dependencies. Basically with a symbol server you can reference a dll in your project, but you can debug original source code as if you have the original project linked instead of having the dll.

Sometimes this process just don’t work. Recently I’have a customer that had problem with this scenario, and the real strange stuff is: I’m able to step in dll source code without problem from any machine, but noone of the customer’s developers are able to make it work. After I’ve sent them detailed instruction it worked, and we were able to track down the problem.

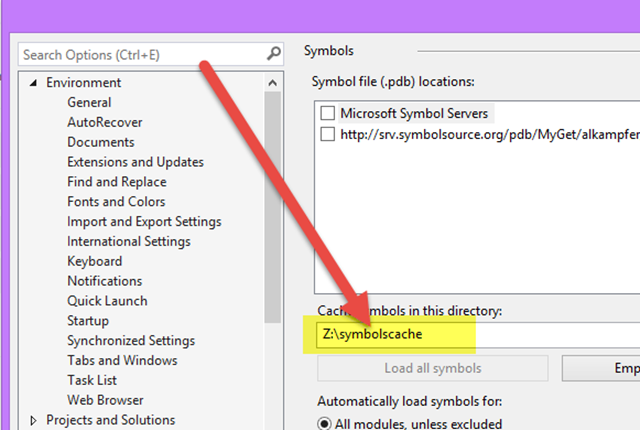
Visual Studio has a nice option to cache symbols in local directory to avoid downloading each time from the server. Here are my usual settings.

Visual Studio options to use local folder as a symbol cache

Figure 1: Visual Studio symbols settings

Developers in customer sites decided to use a subfolder of %TEMP% directory and this was the cause. As soon as they moved symbol cache to something like c:\symbols everything starts working. The underling cause is probably due to long paths.

If you have problem using symbol server, try using a really short path for your Symbols Local Cache directory.

In this specific situation we are using free symbols server in conjunction with MyGet nuget package feeds. In my machine here is the location for a source file during debugging.

Z:\Symbols\src\pdbsrc\MyGet\alkampfer\11111111-1111-1111-1111-111111111111\BIGEND\GianMariaRicci\Jarvis.Framework.Kernel\2C5AB5CBD1C74688974B2DDB55F51EDA1\Jarvis.Framework.Kernel\ProjectionEngine\ConcurrentProjectionEngine.cs

Usual %TEMP% variable is something like c:\users\gianmaria.ricci\appdata\local\temp (this is my system and it is long 44 characters), so it is not a good idea to use it for symbol source cache.

Since it is really easy to have really long path for your source when you use a symbol server , it is always a good idea using a short path for symbols cache directory, something like x:\SymSrc is probably the best solution.

If this does not solves your problem, another suggestion is using Fiddler to inspect the traffic between your Visual Studio and the Source Server to understand what is happening.

Gian Maria.